New frontiers for bright radiation

How can we leverage recent and surprising cost reductions in diode lasers? Here we look at possible applications in the chemical industry: efficient volumetric heating, targeted pyrolysis, faster ethane cracking and other topics. It’s an area with incredible promise, but as far as we can tell still missing its “killer app”.

Brief

The price for semiconductor laser diodes that are bright, efficient (70%), and long-lasting (10-20 yr) is rapidly approaching $1/W. This should mark a paradigm shift in how we view lasers: the cost of the electricity to drive them could soon dwarf their CapEx, making lasers a viable option for electrified chemical or materials processing. Lasers can deliver unprecedented power intensities volumetrically to a suitably absorbing fluid; they can be rapidly steered and modulated to uniformly heat, e.g., a catalytic surface, or to selectively heat inhomogeneous targets (e.g., to pyrolyze inhomogeneous organic waste feedstocks into more valuable bio-oils, or to pyrolyze gaseous hydrocarbons into low-cost carbon fibers). Most tantalizing, lasers can also drive non-equilibrium processes that would make them not just convenient way to deliver energy to chemical streams, but paradigmatically better ways to drive important reactions at scale.
 
In a chemical industry that’s so desperate to electrify that it is willing to throw billions after far- fetched schemes [1], the size of this laser opportunity is hard to overstate. But it’s also one to evaluate as soberly as possible. The semiconductor lasers that are farthest down the cost curve operate in the range 780 – 980 nm, which constrains the materials that can be efficiently processed. Laser systems could be resistant to coking, but optics could be vulnerable without special reactor design. Thermal processes can benefit from low-cost heat storage, whereas laser-driven systems cannot. And of course, the economics of electrifying any process that’s currently driven thermally may stay dodgy as long as the majority of US grid electrons still come from fossil combustion.

‍
Lasers for chemical processing

Overview

Certain varieties of highly efficient near-infrared laser diodes appear to be riding a photovoltaic-like cost curve; they’re getting cheaper to the point where their CapEx could be well below the cost of electricity to run them [2]. It’s now possible, for instance, to put a megawatt of continuous wave (cw) optical power, generated with 70% wall-plug efficiency and tuned to a few-nm-scale molecular absorption band, down a meters-long reactor tube with few-cm-scale diameter and have the light stay basically collimated. What does this enable?

‍
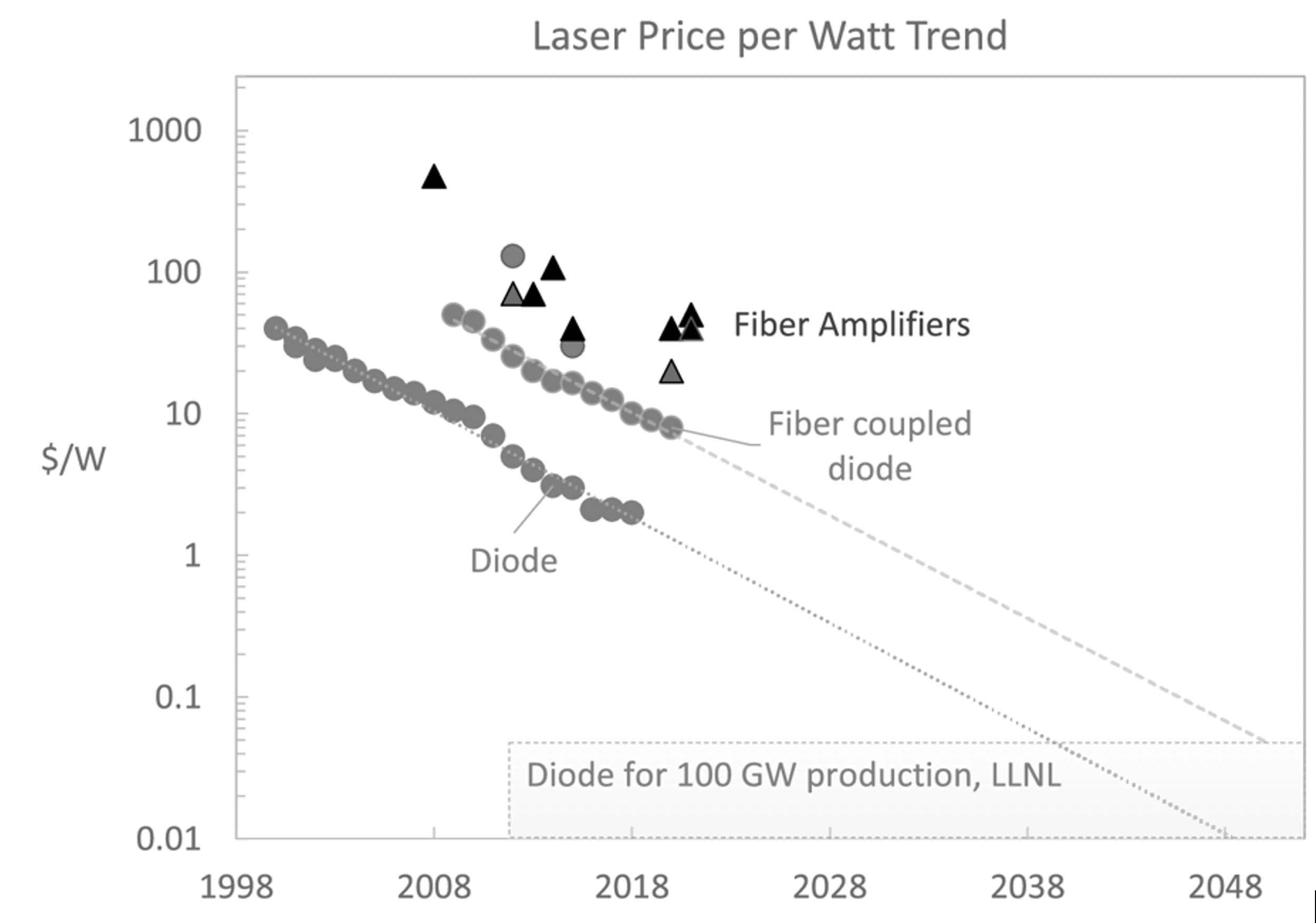
First and foremost, the light could be used as heat. Near-infrared light is absorbed by several molecules of practical interest, including hydrocarbons, H2O, H2S, and (comparatively weakly) O2 and CO2. We will argue that such laser heating could be uniquely enabling for a class of endothermic, uncatalyzed, gas-phase reactions—perhaps sufficiently enabling to justify the cost of electricity even for heating, a task which is often accomplished industrially at far lower expense by burning fossil fuels. We’ll illustrate the utility of laser heating in two example reactions: methane pyrolysis and steam cracking.
 
Second, and more tantalizingly, the non-equilibrium effects of laser light could open up entire new classes of reactions to high-efficiency electrification. Because NIR photons transfer eV-scale energies to specific (typically vibrational) modes of specific molecules, one could use a laser to pump enough energy into a particular chemical species to drive forward a particular reaction without driving others (e.g., reverse reactions or side-reactions). This scheme is often inefficient: for many reactions of interest, the energy of a NIR photon (1-1.5 eV) is too low to drive the reaction forward with high probability before the imparted energy is lost to the reservoir, while the absorption cross-sections are typically too small for multi-photon absorption to make practical sense. Non-equilibrium laser schemes could find more utility in situations that tolerate substantial inefficiency, such as triggering chain reactions (We’ll propose ethane cracking as an industrially relevant example) or in performing high-value reactions in dilute mixtures (e.g., methane scavenging, hazardous waste cleanup).

A handful of these concepts could be the basis for clean-tech startups—most notably the concepts around methane pyrolysis and steam cracking (both quasi- and non-equilibrium). We’ll point out some key technical elements that would need to be derisked. As hinted above, the laser approaches here can be briefly taxonomized as either equilibrium (with all laser energy thermalized in the mix) and non-equilibrium (laser energy partitioned into target molecules in favorable ways). We’ll start with the easier-to analyze equilibrium cases, and then move into the higher concept ideas.

Equilibrium: heating with lasers

An oft-cited step on the path to decarbonizing the chemical industry is to electrify heat, which will make sense in some allegedly forthcoming world of decarbonized grids. If we want to nudge the industry toward electrified heat today, we need a good motivation—and it’s easy to appreciate why, generally, such motivation simply isn’t there. Converting fossil fuels to electricity at a power plant, delivering this electricity to a chemical facility via the grid, and converting back to heat again wastes about two thirds of the heat of combustion. Electricity prices furthermore reflect the CapEx and OpEx of the power plants and grid, and that’s assuming the grid can even handle the plant’s electricity demand. The net result is that electrical heating is often several times costlier, per unit of heat energy, than direct combustion. Electrified heat looks like a crummy deal for any low-margin business, even before considering that with the fossil-dependent grid in most parts of the world, it might even be worse for the climate.

Yet there are cases in which an electrified heating apparatus offers such a critical advantage that the electrified option is industrially preferred. The electric arc furnace, commonly used in steelmaking, is a notable example. The arc furnace finds utility here because it can deliver extremely high power densities to remelt bulk steel scrap while remaining scalable, low-cost, and compatible with intermittent operation. By comparison, traditional steel furnaces need to run continuously, are more economical at large scales, and derive heat from combustion of carbon distributed throughout the bulk, which limits their use of scrap steel. Evidently the dynamics of the industry are such that the specific advantages of the arc furnace can make up for the higher cost of energy.
 
(Various decarbonization startups like Lydian are of course betting on this being true for a wider variety of reactions as electricity prices fall and carbon prices rise)

Analogously to the arc furnace, there are crucial advantages of laser heating—principally its high power density—which could give it a toehold in certain industries, especially those which rely on endothermic, gas-phase reactions. I’ll illustrate this concept with a couple of case studies: steam cracking and methane pyrolysis.

Steam cracking

Steam crackers carry out the pyrolysis of alkanes (e.g., ethane) to olefins (e.g., ethylene, propylene). The pyrolysis reaction initiates at high temperatures, but if high temperature is held for too long, the olefins themselves start to degrade to products like acetylene and soot. Hence the highest yields of olefins are obtained when the process gas is very rapidly ramped and quenched; a typical steam cracker ramps its process gas from ~600 C to ~850 C over a few hundred milliseconds, and quenches back down to 500 – 600C within another hundred milliseconds.

In order to achieve such a rapid temperature ramp with high throughput [3], a steam cracker will push the process gas near the speed of sound through long (10 – 100 m), narrow (~10 cm diameter) “cracking coils” maintained at a high temperature (e.g., 1000C) by a firebox. A severe drawback of this scheme is that, since the coils must be particularly hot (hotter than the process gas) in order to rapidly supply heat, they act as excellent nucleation sites for coke deposition. And since coke is a poor thermal conductor, the temperature of the coils must be further increased once coke starts to deposit. Increasing temperature decreases coil lifetime, and this can only continue for so long before it becomes economically advantageous to shut down the entire steam cracker to clean out the coke. The shutdown typically costs two days, and happens once every few weeks to few months, depending on the length of coil (diabolically, shorter coils reduce residence time and improve yield, but require higher temperatures and therefore coke faster). Decoking shutdowns are a major operational expense to go along with the capital expense from the massive fireboxes, long coils, and powerful pumps that drive the large fluid impedance.

A laser heating approach could circumvent these issues. A NIR laser may be able to deliver an average intensity ^[4] of 1 MW/cm^2 to the gaseous steam/hydrocarbon mixture, whereas the coil surfaces might deliver only 10 W/cm^2. Since the coils radiate in the mid-IR, whereas the NIR laser would likely be tuned to water absorption at 950 nm where the optical cross-sections are ~300x lower, the relative volumetric power delivery advantage of the laser can be estimated as (1 MW / 10 W) / 300, or roughly 300x. This is a sizeable margin that could allow a laser reactor to dispense with long, narrow coils and reduce pumping requirements. The walls of the reactor would not be hot, and could be coated with arbitrary anti-coking materials (whereas coatings on coils need good thermal conductors), and the laser reactor tubes could be short and wide. The laser reactor would thus be far less affected by coke deposition, mitigating the operational losses associated with decoking while still permitting very short residence times for high yield.
An even more stripped-down version of laser-assisted alkane cracking can be imagined which gets rid of the steam dilution apparatus entirely, further saving CapEx. One function of the steam ^[5] is to act as a diluent, which is supposedly helpful since low hydrocarbon partial pressures favor the unimolecular decomposition reactions over the unwanted secondary multi-molecular reactions. Simply lowering the pressure of the ethane is impractical because the pressure drop across the coils is so large, in some cases as high as 1 atm ^[6]. Another function of the steam is to combat coking via a water-gas shift reaction. These functions may no longer be needed in a laser reactor, in which both the pressure drop and the coking (and the extent we care about coking, as long as it isn’t on the optical window) are greatly reduced. The laser would instead heat the alkanes; a practical challenge here is that the optical cross-section of alkanes may be severalfold lower than that of water, which increases the absorption length ^[7]  and introduces more concerns about the effects of turbulence on beam quality.

It's not obvious whether or not the above CapEx and operational advantages of the laser reactor could justify the use of electricity. Assuming that heat exchangers bring the process gas up to 600 C, and that lasers are only used for the high temperature step, and that the single-pass conversions are reasonably high (>50%), the laser will be required to deliver ~150 kJ/mol C2H4 (i.e., mainly the enthalpy of reaction). At 50% overall wall-plug efficiency this is 300 kJ/mol C2H4 = 11 MJ/kg C2H4. If we had to accept present-day average industrial utility costs of $0.07/kWh, the electricity would cost $0.21/kg C2H4, and ethane feedstock might be around $0.25/kg C2H4, totaling $0.46/kg C2H4 from these inputs alone; we could sell [8]  our H2 to defray maybe $0.10/kg, leaving us at $0.36/kg C2H4 before including CapEx and the OpEx for balance of plant. It’s a little alarming that the true sale price of ethylene ranges from $0.40/kg to $1/kg, as we’re pretty close to the low end of this already. But before concluding that we’re not competitive without a hefty green premium, more research into the true technoeconomics of traditional steam crackers is in order: these plants may well be running at a loss when the sale price is $0.40/kg. It’s also worth noting that a decent ethane cracking plant consumes something like 16 MJ of fossil energy per kg ethylene produced, so our 11 MJ/kg C2H4 laser process, plus some nontrivial additional energy cost for balance of plant, could easily become a worse carbon emitter than a traditional steam cracker if we’re getting electricity mainly from fossil fuels.

The laser process looks more appealing if it can operate intermittently, taking advantage of either low-cost renewables (which would make the decarbonization argument quite strong) or at least a lower cost of electricity, as in the case of the electric arc furnace for steelmaking. This might be feasible if our design really saves a lot on CapEx in the ways suggested above. We would likely still use cryogenic separation, which is less advantageous to run intermittently, but perhaps we could devise a way to safely store our products before they’re fully separated, and run separation jobs in batch, accepting the higher electricity costs for this part of the process. Achieving low CapEx could enable us to respond to demand: if CapEx is low enough, we could let the facility sit and avoid production until ethylene prices recovered to a profitable level. A detailed technoeconomics of the best-case laser reactor should be performed to explore these arguments further. The likely truth is that the CapEx of steam crackers is low enough that it won’t be possible to displace them on CapEx alone. I estimate ~$1B for a million-metric-ton-per-year plant using scaling data, which amounts to a few pennies per kg amortized over a few decades of operation.

Methane pyrolysis

The electrified pyrolysis of methane (or other hydrocarbons) yields blue hydrogen along with carbon-containing species whose chemical identity depends on reaction conditions; examples of valuable pyrolysis co-products include carbon black and acetylene ^[9]. Lots of startups are onto this: CZero, Molten, Modern Hydrogen, and Monolith are notable examples, all with different schemes to heat methane without oxidizing it (some in molten metal, some in plasmas, some via steam reforming and then the Boudouard reaction). None can survive as a company without either a subsidy or sale of a valuable co-product: pyrolysis only gives you 2 H2 per CH4, and on that basis loses out to the incumbent steam methane reforming, which gives 4 H2 per CH4. Despite this, none of these new approaches appears particularly well optimized for delivering a valuable carbon co-product.

Carbon black

Carbon black is often used to reinforce tires, or as a pigment. It is primarily produced using the “furnace black” method: liquid hydrocarbons are fed into a natural gas flame, which pyrolyzes the liquid hydrocarbons into carbon black particles. The particle size can be tuned by changing the quench conditions (typically water injection), residence times, or reactor geometries. The production method is not emissions-friendly, and the purity of these carbon blacks is not the highest, owing to the presence of oxygen and the use of liquid feedstocks. But if the reaction heat is to be supplied by a burner, there aren’t many compelling schemes that effectively heat the gaseous feedstock other than direct injection into the flame ^[10].
 
More options open up if the reaction heat is delivered electrically. Plasma reactors based on arc discharge or microwaves have been used for decades to deliver high-temperature heat to gaseous feedstocks at high power densities, but only recently has anyone claimed to have developed an industrially compelling “plasma black” process. In Monolith’s scheme, one or more hydrogen plasma torches feed hydrogen plasma into a stream of natural gas, which pyrolyzes into more hydrogen and rather pure carbon black [11]. By tuning the plasma parameters (e.g., hydrogen flow rate, power), Monolith claims to be able to produce different grades of plasma black (corresponding to different morphologies, etc.). They further claim that their plasma black is particularly effective in reinforcing tire rubber, and that they will be able to sell both carbon black and hydrogen at prices that compete with today’s comparatively dirty processes.

“Laser black” produced from natural gas could be even more appealing. In this scheme, a NIR laser tuned to the absorption bands of methane (e.g., near 890 nm [12] ) would deliver heat with a very high power density to a continuous stream of natural gas in a simple tubular reactor with appropriate optical access. Many experimental knobs would be available: pressures [13], flow rates, beam geometry/power density [14], feedstock preheating, hydrogen input, optional quenching schemes, etc. This is arguably a richer design space than the plasma black process. Since the materials science of carbon black and the chemical mechanisms controlling its production are not tremendously well understood, it’s anybody’s guess whether laser black ends up being more or less valuable than its peers. One reason for optimism is that a thermal pyrolysis process is expected to form acetylene as an intermediate, which then decomposes to carbon black [15]; the thermal decomposition of acetylene is known to form a more graphitized and conductive carbon black (“acetylene black”) valuable to the semiconductor, electronics, and battery industries. The existing market for acetylene black is admittedly small, but it’s conceivable that the product could be more widely used if it were available at lower cost or could be tailored for other applications (e.g., tires). 

The laser process stands to beat Monolith’s process on price owing to several operational advantages. One is that, owing to the simplicity of the reactor, there should be minimal delays for cleaning, as long as all optical surfaces can be kept clean of soot (a big if, but appropriate selection of materials, reactor and flow geometries, active anti-soot countermeasures, etc. could overcome this issue). Monolith apparently plans for substantial downtime—as much as a few days every two weeks—for cleaning reactors and replacing plasma electrodes. The laser reactor could also naturally leverage heat exchangers to reduce the energy bill for its fully thermal process [16].

Acetylene

Acetylene is produced from one of three modern processes: the calcium carbide process, arc discharge in hydrocarbons, and as a byproduct of steam cracking. Its use as a chemical intermediate has declined since the 1960s owing to the increasing availability of lower olefins from steam cracking, but acetylene torches are still useful for their unsurpassed flame temperature. One of the key drawbacks to acetylene in general is its explosive character, which makes it expensive to store and transport. If acetylene could be produced in a more distributed fashion from electricity and ubiquitous natural gas, thereby avoiding the long-distance transport problem and mitigating the storage problem, it could likely find more commercial use. (Whether the co-produced blue hydrogen is useful in this scenario or whether we really want the world to use more acetylene are valid but separate questions that I won’t try to answer here.)
 
A similar laser pyrolysis reactor to that imagined for carbon black could be applied to acetylene production. Thermal pyrolysis of natural gas, which proceeds above 1000 C, is thought to lead first to ethane, then rapidly to ethylene, and then to acetylene. By rapidly quenching the process gas—for instance by direct injection of additional feedstock, inert gas, etc., at the cost of additional downstream processing—it’s conceivable to produce high yields of acetylene, with some likely production of carbon solids [17].

As was the case with carbon black, a plasma approach would again be the competition. Plasma has been applied to produce acetylene from hydrocarbons since the 1940s, with several industrial facilities built (tens of kta) using electric arc discharges. These reactors achieve 30-45% energetic efficiency of conversion from feedstock to acetylene, with ~80% selectivity of acetylene over other hydrocarbons in the output stream. A recent startup called Transform Materials, which appears to be similarly motivated to provide distributed acetylene production from natural gas, claims to have built a modular microwave plasma reactor for this purpose. Their claimed energy efficiencies are in line with old literature (~40%), with slightly higher acetylene selectivity (90-95%).
 
Whether the laser or microwave plasma pyrolysis works should work better for distributed acetylene production isn’t clear to me a priori. The efficiency of the laser process isn’t likely to be better, given that the wall-plug efficiency of the laser itself is probably 70-80% at very best, whereas Transform claims that their 100 kW magnetrons are 90% efficient and that the energy is delivered to the plasma with very small loss. There might be some operational advantages of the laser, depending on how problematic the window soot is (see earlier comment): whereas the plasma reactor must stop operations for a few minutes every hour and switch process gas to burn off soot deposits in the narrow reactor tube, the laser process could be less sensitive to clogging/fouling by using a much wider reactor tube and a much lower reaction temperature (Transform’s gas temperature is 3000 C). The laser process might save a bit of energy and CapEx because it can operate at higher pressure, whereas Transform’s plasma must operate at about 0.1 atm, as is typical for plasma processes. Yet a lower pressure might favor acetylene production (advantage: plasma).
 
We consider the case for distributed acetylene production by any method to be somewhat suspect, and the case for lasers improving on plasma here looks shaky. It’s nonetheless an example of a process where an electrified solution could make sense owing to the involvement of an endothermic, gas-phase reaction.

Non-equilibrium

Although lasers could be interesting for particular heating applications, as discussed above, it is the non-equilibrium aspects of laser chemistry that have received the most attention. I’ll take a closer look at several of these areas in the sections below and evaluate whether there’s any connection to commercial utility. I’ll skip discussion of the well-trodden areas of photochemistry and photocatalysis, which in any case require more energetic photons than those available to us from our low-cost NIR diode lasers.

The holy grail: selective bond rupture

A longstanding goal of laser chemistry is to break specific bonds within specific molecules in a mixture, selectively triggering reactions [18]. The idea is simple: since infrared laser light couples into specific vibrational modes, it should be possible to excite, for instance, a C-H stretching mode to the point of dissociation, while leaving other bonds intact. But the practical relevance of this concept has so far proven limited. The trouble can be traced in large part to anharmonic coupling between the different vibrational oscillators of a polyatomic molecule, which rapidly redistributes vibrational energy between the vibrational modes; these timescales are often sub-picosecond, and likely even shorter near dissociation. Under such conditions only ultrashort and ultra-high-power lasers can even theoretically pump dissociation-level energy into the mode of interest. Anharmonicity also means that the energy gaps between successive vibrational modes for a given oscillator are not constant, but instead vary with oscillator quantum number. As a bond absorbs more vibrational energy, the spectral position of the relevant absorption lines will therefore shift. This makes it difficult to “climb the quantum ladder” to dissociation using photons of a fixed, narrow frequency range.

The next closest thing: vibrational catalysis

A more tractable incarnation of these non-equilibrium concepts—which I’ll refer to loosely as “vibrational catalysis” (in what I think is a slight abuse of the term “catalysis”)—might be to pump energy into all vibrational modes of selected molecular species and hope that this helps overcome an activation barrier to a reaction of interest. Although less powerful than the holy grail mentioned above, vibrational catalysis could still be preferable to a fully thermal process in some cases. As an example, consider the water molecule. Water has 3 translational, 3 rotational, and 3 vibrational modes. Let’s say a reaction is known to proceed from a particular activated configuration of water, which is reached when a minimum energy  partitions itself into certain vibrational modes. Now consider two baths of water: the first contains a thermal distribution of water with average energy  partitioned across all 9 modes, whereas the second contains water at an elevated vibrational temperature with average energy  confined to the 3 vibrational modes. A water molecule randomly selected from the thermal bath has a miniscule chance of being found in the activated configuration, which corresponds to a tiny subset of the possible microstates, whereas a water molecule randomly selected from the vibrational bath has orders of magnitude larger chance of being in the activated state because the state space is much smaller. In this way, vibrational catalysis could lead to a much higher rate of forward reaction than in a fully thermal process, given identical energy input [19]. In practical terms, this could mean improved energetic efficiency, or the ability to drive reactions that would otherwise call for inaccessible temperatures [20]. Another potential advantage of vibrational catalysis—depending on the selectivity of the excitation mechanism—is the ability to drive desired forward reactions involving certain species without driving reverse or other off-target reactions.

The concepts behind vibrational catalysis have been explored using non-thermal plasmas [21]. Under certain plasma conditions, it is thought that electrical energy (e.g., from microwaves) can be pumped almost exclusively into the vibrational modes of specific molecules. The most notable example of plasma-based vibrational catalysis carries out the reaction N2 + O2 -> 2NO, which would require several thousands of degrees Kelvin to go forward in a thermal process owing to the large (~10 eV) energetic barrier for cracking nitrogen [22]. The energetic efficiency of the non-thermal plasma is claimed to be 30% of the thermodynamic limit, with a much higher conversion than any thermal process under practical conditions [23].
 
A laser-based implementation of vibrational catalysis offers some key advantages over its plasma counterpart. The excitation mechanism of the plasma is rather unselective. Although in some cases, like with nitrogen/oxygen plasma, it’s possible to excite electrons in such a way that most of the delivered energy goes to the vibrational modes of a desired species, this is not generically possible to do. In some molecular mixtures, the conditions appropriate for vibrational excitation of one reactant species lead to unintended excitations of another (e.g., rotations, electronic excitations, ionization). The excited electrons will inevitably excite the product species as well, potentially initiating reverse or off-target reactions. There’s no good way around these problems other than to be very selective about which reactions are attempted. On the other hand, so long as the molecules have infrared active modes, lasers can theoretically deliver vibrational energy to the reactant species in arbitrary ratios. With some luck regarding absorption spectra, the lasers can avoid or at least mitigate excitation of the products.
 
Despite these considerable advantages, laser-based vibrational catalysis looks like a technical longshot without major advances in laser technology. The basic trouble is that a single NIR photon—which is the only type of photon we can currently hope to supply with any reasonable combination of wall-plug efficiency, optical intensity, and capital cost—often does not carry enough energy to overcome an activation barrier. Multiphoton absorption is therefore required, and this is hard to do efficiently.

Let’s take methane as an illustrative example. Activation barriers might be ~4 eV, corresponding to the strength of the C-H bond [25]. For a thermal population near room temperature, an average methane molecule with 9 modes at 25 meV each will carry less than a quarter of an eV of total energy. To excite the average methane molecule to ~4 eV will therefore require three or four NIR photons to be absorbed before the vibrational non-equilibrium dissipates into the bath. Given a vibrational-translational (V-T) relaxation timescale of 2 us-atm for methane near room temperature [24] and a practical operating pressure ~1 atm, we have ~2 us to absorb our three or four photons into a given molecule. Owing to anharmonicity (as well as multiplicity considerations to be explained shortly), the optical absorption spectrum of a molecule that has absorbed the first NIR photon should be quite different from that of the average thermal molecule. At first blush, this looks to be a feature rather than a bug: because the spectral shift distinguishes molecules that have previously absorbed photons, it could be leveraged to further excite only these molecules. Without such a feature, we’d have to indiscriminately supply all (or most) molecules with 3-4 eV within our V-T relaxation window; if we tried to do this with NIR lasers, we’d quickly blow through various practical limits owing to the small optical cross-sections [26], and even if we succeeded, we’d be left with lots of excess energy to dissipate [27]. But even with our spectral selectivity, it won’t be easy to efficiently absorb the next photons into our excited molecules. Let’s say we only excite 0.1% of our molecules within a single V-T lifetime, skirting the problematic intensity requirements articulated in the footnote above. Now the optical absorption lengths for the second NIR photon are at least a thousandfold longer [28].They were already problematically long to begin with at >10 m for 1 atm; I doubt there’s any practical way to fold the optical path enough to reliably get 10 km of propagation through our turbulent mixture.

The moral of the methane example is that multiphoton absorption with NIR light is going to be tremendously inefficient. The NIR optical cross-sections for most other molecules of interest are not more than an order of magnitude larger than those for methane, and thus not sufficiently different to change the qualitative conclusions. Multiphoton absorption is also probably required in most cases; if activation barriers are only ~1 eV, reasonable reaction rates should already be obtainable at pretty low temperatures, and there would be less reason to turn to non-equilibrium chemistry.

The appeal of multiphoton absorption could change a bit if we could use the mid-IR instead of the near-IR. In the mid-IR, absorption cross-sections are five or six orders of magnitude larger, which brings the required optical intensities and absorption lengths into far more reasonable territory. If we could make low-cost (~$1/W), efficient (60-80%) lasers at a judiciously chosen set of mid-IR wavelengths, it could be very interesting to explore whether one could efficiently implement the multiphoton absorption scheme imagined here. Alas, no such lasers are currently available, and the ideas being pursued in academia don’t look terribly promising [29].
 
Before launching a heroic quest to build the perfect mid-IR laser, it’s worth acknowledging one general limitation to the utility of any vibrational catalysis scheme. Roughly speaking, vibrational catalysis amounts to paying electricity to do a catalyst’s job. Whether this makes practical sense depends on how expensive the candidate catalyst is, and how much excess energy must be spent per molecule to push the system over the activation barrier. In many cases—including that of the famous NO-from-air plasma—the excess energy amounts to multiple eV per product molecule, which is often multiple times . Unless this excess energy can be recovered as high-temperature heat, which may not generically be possible, we can expect a big efficiency hit. Considering that whatever is delivering the energy (e.g., a laser, magnetron, gyrotron) will suffer further losses converting electricity to vibrational energy, it’s easy to appreciate why vibrational catalysis might be too expensive for many applications, especially in commodity processes.

Vibrational catalysis for chain mechanisms

Vibrational catalysis as imagined above may be crippled by a need for multiphoton absorption and a steep efficiency penalty. But these drawbacks aren’t relevant in all cases. One notable example, explored here, is if vibrational catalysis is used to trigger a chain reaction. If the chain length of the reaction is sufficiently long, we only need a small fraction of the reactant molecules to be triggered, and this process need not be efficient.
 
Let’s revisit ethane cracking as a possible use case for our non-equilibrium scheme. Ethane pyrolysis is a chain mechanism, [30,31] thought to be propagated by ethyl radicals (C2H5) via the unimolecular decomposition C2H5 → C2H4 + H and the abstraction H + C2H6 → H2 + C2H5. These reactions are believed to proceed for long chains, terminating principally by the recombination of ethyl radicals to form butane, 2 C2H5 → C4H10. The initiation step involves the unimolecular decomposition of ethane into methyl radicals C2H6→ 2CH3; the methane radicals then attack ethane to form ethyl radicals via the reaction CH3 + C2H6 → CH4 + C2H5. Splitting ethane into methyl radicals carries by far the biggest activation barrier (3.7 eV) of all reactions involved in this mechanism.

In the typical steam cracking of ethane, process gas is heated to 500-600 C in the “convection zone” of the furnace, then very rapidly ramped up to 800-900 C in the radiation zone to perform the cracking, and then rapidly quenched back to 400-600 C to avoid side reactions such as the formation of acetylene or solid carbon. Inspection of Arrhenius data [32] suggests that at 600 C, only the initiation step C2H6 → 2CH3 is particularly slow, owing to its large activation barrier, with a rate constant 4e-5/s. The next slowest step is the unimolecular decomposition of C2H5 in the chain mechanism, whose rate at 600 C is estimated to be nine orders of magnitude faster: 5e4/s. It thus appears that a key reason to use high temperatures in the steam cracker is to overcome the 3.7 eV activation barrier in the initiation step.
 
What if instead we used vibrational catalysis to trigger the initiation step while holding the process gas near 600 C? If it worked, this scheme could hugely simplify the cracking apparatus by eliminating the need for high-speed fluid flow and quenching/heat recovery hardware, thereby saving on CapEx and energy. The absence of the high temperature step might greatly reduce coking, which would be a major operational advantage in the context of quasi-equilibrium laser heating. The suppression of coking might make it possible to eliminate the steam circuit entirely (as discussed above in the Equilibrium section).

What follows below is a crude feasibility study using basic statistical mechanics, the classical RRKM theory of unimolecular decomposition, and Arrhenius parameters from literature. These numbers suggest our concept could be viable (but I should emphasize that it’s a sketchy analysis). When ethane at 600 C is irradiated with 1.4 eV light (880 nm), about 1 in 100 input photons could trigger chain reactions. By appropriate tuning of the optical intensity, it’s possible to make the chain length ~ 100, so that the excess energy from the photons which don’t trigger chain reactions will supply the heat of reaction (very close to the photon energy) rather than raising the temperature of the gas. This process can be run at practically useful overall reaction rates (C2H6 → H2 + C2H4) around 0.25/s. A challenge with our method will be the rather long absorption length, which could be 100 m in ethane at 1 atm (I don’t have the exact data). But it may be possible to build suitable reactors.

Gory details

Let’s appeal to the classical RRKM theory [33] as an easy (but potentially incorrect) starting point. This theory describes the rate of unimolecular decompositions under the assumption that in order for the decomposition reaction to occur, one specific vibrational oscillator must carry the entire activation energy. Working through the combinatorics (n balls in s energy bins) reveals that this constraint is satisfied a fraction ((E-Eo)/E)^(s-1) of the time, where E is the total energy stored in s modes, and Eo  is the activation energy. This implies that the reaction rate is vanishingly small if the molecule only has just enough energy to reach the activation energy, which makes sense, since in this case there are vanishingly few ways to distribute the energy to reach the appropriately activated complex. The more modes, the more energy is required for a reasonable probability.

In the high-pressure limit, the overall rate of reaction can be shown to take the Arrhenius form, k = v e^(-Eo/(kT)), where v is the attempt frequency. Experimental fits using these parameters  and  often leads to the finding that  is a few orders of magnitude larger than what might be expected (e.g., a thousand times the thermal frequency) and  is about half of what is expected from counting the vibrational modes. Specifically for ethane near 600C, Laidler [31] suggests s = 9, Eo = 3.7 eV, and v = 10^17/sec.

What is the minimum energy an ethane molecule must have such that when hit by a 1.4 eV photon, it will decay to 2CH3 with near-unity probability? Ethane has a short V-T relaxation time [24] of ~20ns near 600C and 1 atm (we’ll choose this pressure for now). Naively applying RRKM concepts, the rate of reaction for a molecule with energy E > Eo is v((E-Eo)/E)^(s-1). (This formula, along with its unphysical , may well characterize ensemble properties, but it strikes me as misapplied in the present single-molecule context. I haven’t thought up a better alternative, so I’ll forge ahead with this estimate, keeping in mind this major caveat.) We might require that this rate exceeds the relaxation rate by a factor of ten, i.e., v((E-Eo)/E)^(s-1) > 1GHz, which is satisfied for E>4.1eV. This naïve assessment suggests that a molecule with energy E* = 2.7eV would likely convert to 2CH3 when struck by a 1.4 eV photon.

At 600 C, the fraction of molecules that have E > E* = 2.7 eV is, within a crude classical model

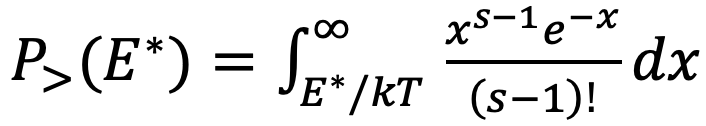
The choice of s is important, but it isn’t obvious which value best mimics real properties of the gas when quantum effects are considered. If we select s = 3N = 24, which represents an optimistic case [34], we find P>(E*) = 0.01; a more pessimistic choice [35] might be s = 13, in which caseP>(E*) = 3e-6. I’ll do the analysis below with the optimistic case. If we want to keep the temperature constant despite triggering only 1% of molecules into a chain reaction for each 1.4 eV photon supplied, we will need the chain length to be ~100 (i.e., each ethane molecule decomposed to 2CH3 triggers ~100 to convert to C2H4); this works because the enthalpy of reaction is so close to the photon energy. Given a rate constant 5e4/s for the chain propagation step at 600 C, we therefore need the chain termination rate to be 5e2/s. The bimolecular conversion of an ethyl radical to butane (i.e., chain termination) proceeds at a rate ~1e8/(s-atm) per literature [31, 36]. At our total pressure of 1 atm, we thus require an ethyl radical volume fraction (5e2/s) / (1e8/s) = 5e-6. If we maintain this fraction of ethyl radicals, the conversion rate of the net reaction (C2H6 -> H2 + C2H4) is 5e-6*5e4/s = 0.25/s, which seems practical.

One major experimental challenge, though, pertains to the absorption length in ethane. We don’t exactly know the absorption cross-sections at this stage. Above I’ve used a rough figure 1e-23 cm^2 for NIR cross sections, but in this case, since we’re chiefly trying to get the higher energy molecules in the thermal bath to absorb our photons, the relevant optical absorption features might shift or broaden away from the main blob that looks like 1e-23 cm^2. If we take 1e-23 cm^2 as an upper bound on the cross-section, we already need ~100 m of propagation through 1 atm of ethane to absorb most of the photons. We’ll clearly need to fold our optical path many times to have our scheme work efficiently, which can be a practical challenge (but not an impossibility) owing to beam divergence, turbulence, and deposition on optical surfaces [37]. On the plus side, the laser intensity required for our process is [38] a very reasonable 6000 W/cm^2.

Another issue with this low temperature cracking approach might be the extended lifetime of the intermediate radical, C2H5, which could leave more room for secondary reactions. The decomposition of C2H5 happens about 60 times faster at 800 C than it does at 600 C. This is significant because if ethylene is floating around, we could also have C2H5 + C2H4 → C4H9 in addition to the decomposition and chain termination steps mentioned above [39]. The ethyl-ethylene reaction might yield unwanted byproducts; I haven’t yet found good Arrhenius parameters with which to estimate the severity of this problem. In theory we could try to accelerate the C2H5 decomposition using lasers, but in practice I suspect this will be hard because ethyl will be at a low concentration. (Maybe we could hasten the decomposition using a MIR laser tuned to a C2H5 transition, but given the efficiencies of such lasers, and given that 1 ethyl radical yields only 1 ethylene molecule, we wouldn’t want to supply more than one or two quanta per ethyl radical to stay efficient.) It would also fix our problem if we had a membrane that could separate out C2H4 as the reaction went on, and worked at 600 C, but no compelling membrane material seems to exist yet (if it did, we might already be trying to use it as a replacement for cryogenic separations in conventional steam crackers).
 
From the perspective of reducing side reactions, we’d also probably want to tune our laser such that we mostly absorb the photons in ethane rather than in ethylene. I’m not sure how possible this is; good spectra near 880 nm aren’t available, especially for our temperature range. You’d think there would be some shift—at least a few nanometers—between the overtone bands for ethane and ethylene owing to the CH3 vs CH2 groups.

A variant of our scheme might be to use both a NIR laser in combination with a weaker, MIR laser that is tuned to a resonance accessible primarily to highly excited molecules. The NIR laser efficiently delivers a handful of vibrational quanta, while the MIR laser delivers one more quantum, with lower efficiency but much higher absorption cross-section. The MIR laser further encourages the initiation step and is used sparingly – e.g., it could target only the ~4e-5 most excited ethane molecules from the example above and further encourage them to dissociate. Since relatively little of the total energy is being delivered via this mechanism, it’s more feasible to use MIR lasers with lower efficiency and higher cost per watt. 

Vibrational catalysis for high-value reactions in dilute mixtures
Since laser-based vibrational catalysis is the only technique that can target specific chemical species in a bulk gas, it might be particularly valuable for performing a reaction involving dilute species. I’ll first explore a climate-motivated example: the combustion of trace quantities of methane in air or exhaust gases. Since the GWP of CH4 is 83 over 20 years and 30 over 100 years, it might be seen as worthwhile to combust methane if the needed energy consumption could be kept within a certain budget [40]. Taking the 20 year timeframe, and assuming we want to stay 10x below break-even, our energy budget works out to 100 eV/molecule CH4 if we use solar (0.05 CO2e/kWh) and 10 eV/molecule CH4 if we use natural gas (0.5 kg CO2e/kWh).
 
A thermally activated oxidation scheme would only fit within these budgets for relatively high concentrations of methane, because all gas molecules will receive energy. Consider trying to combust methane near a large methane source where the methane concentration is 100 ppm in air. Using electricity derived from natural gas, our 10 eV/molecule budget gives us 10 eV/molecule * 1e-4 = 1 meV/molecule, which is enough to heat the air by just 3 K. A solar-powered implementation—which would be fraught with challenges related to intermittency—would be able to heat the air by 30 K. Although higher temperatures could theoretically be reached with ultra-efficient counterflow heat exchange, it’s clear that thermal processes do not have much of an energy margin; 100 ppm methane looks like it’s right on the edge of what’s possible to combust, even with a nice catalyst. Lower concentrations look basically out of the question because the available energy is spread even thinner.
 
One way around this problematic concentration scaling might be to deliver energy directly to CH4 molecules, using laser light and vibrational catalysis to induce oxidation. If we could pump enough energy into CH4 molecules to dissociate them to CH3 + H, they might subsequently form CH3O2—the first step in the typical atmospheric mechanism for destruction of methane [41]. In fact, calculations support the dissociation of CH4 under even weaker conditions: CH4 molecules excited to vibrational energies even slightly below the threshold for dissociation might still have a high probability of reacting with O2 before losing their vibrational energy through collisions [42].

For the sake of argument, let’s assume that each CH4 molecule requires ~5 eV within its V-T relaxation lifetime to dissociate with high probability, and that if such energy were delivered, it really would lead to rapid (i.e., orders of magnitude faster than typical 12-year methane lifetime) oxidation to CO2, with no off-target effects. In the vibrational catalysis section, we noted that delivering this energy with NIR light would be crippled by low optical cross-sections; the use of mid-IR was ruled out owing to cost and inefficiencies of lasers [43]. But these cost and efficiency restrictions don’t apply to the methane destruction problem. Consider that with a 10% efficient mid-IR laser (and we have many examples of these—e.g., quantum cascade lasers, optical parametric oscillators) appropriately tuned such that all photons get usefully absorbed, the energy cost to deliver 5 eV/molecule would be 50 eV/molecule, which is within our energy budget if using solar electricity. We would still need to have enough lasers covering enough spectral resonances to efficiently track the anharmonicity, as discussed previously, but this doesn’t inherently increase the cost of the approach [44]. The path length and optical intensity requirements also look tractable: the mid-infrared modes near 3.3 um and 7.6 um have cross-sections ~1e-18 cm^2, which means light will be absorbed within about 10 m for 100 ppm methane, and the needed intensity is below 100 kW/cm^2, which is manageable [45]. It should be noted that both problems get more challenging if the optical cross-sections of excited molecules diminish appreciably below 1e-18 cm^2, which they likely do owing to multiplicity of initial states; this is a major technical/scientific risk. Depending on the exact anharmonic shifts seen by methane, dodging the water absorption features in the mid-IR could be particularly annoying.  

What would our lasers need to cost to make this attractive? The cost of electricity per kg CO2 removed, using the 50 eV/molecule figure above, would be ~$40/ton CO2. If we had a $100/ton CO2 credit, we might suggest that the lasers cost roughly the same as the electricity per ton CO2, leaving a respectable profit margin. Amortizing over 20 years at 25% duty cycle (accounting for solar intermittency), the total electricity used per optical watt (accounting for 10% efficiency) is 440 kWh; the capital cost per optical watt should then be $0.04/kWh * 440 kWh/optical W = $18/optical W. This is 10-100x below today’s price for quantum cascade lasers, but it may look closer in a decade or two. Making a mass-produced mid-IR optical parametric oscillator for around $18/optical watt could be more feasible in the near term, as the pump lasers involved (e.g., YAG or fiber) are already near this cost target, and the nonlinear crystal used might not be a significant expense.
 
From where I stand, methane destruction by vibrational catalysis looks challenging—but not completely impossible—on both scientific and technoeconomic fronts. To further vet this concept we’d need to dig deeper into the optical spectrum of excited methane, which is a challenging domain theoretically and computationally, but there are some useful studies already [46]. We’d also want a clearer picture of what happens after the initial methane dissociation: does this really lead to CO2, and with what off-target effects?
 
A related problem space that could be interesting to explore as a vibrational catalysis beachhead involves hazardous waste cleanup. There are surely many industrial waste streams which must be incinerated because of trace hazardous chemicals; it might be energetically and thus possibly economically favorable to remove these trace chemicals via laser-induced vibrational catalysis.

Wrapping up

Methane pyrolysis is a clear candidate for initial study: a laser pyrolysis reactor could volumetrically deliver heat to drive the highly endothermic pyrolysis reaction, which has been historically tricky to do, owing to the low thermal conductivity of methane. A rudimentary analysis of the laser pyrolysis reactor indicates potential to surpass Monolith’s (and other pyrolysis contenders’) plasma process in efficiency and win on cost. Technical risks include uncontrolled light scattering from turbulent flow, scattering/absorption from particles of solid carbon, and deposition of carbon on optical windows. 
 
In the long run, a laser reactor similar to that imagined for methane pyrolysis could help electrify ethylene production via steam cracking, the leading carbon emitter in the chemical industry. Steam cracking is tricky because the feedstock (often ethane or naptha) must be heated to 800C over a sub-second interval; too long at high temperature will yield unwanted byproducts. Since the cracking reaction is highly endothermic, a parcel of gas traversing the reactor must absorb plenty of heat in that sub-second interval. Traditional steam crackers accomplish this by pushing gaseous feedstock near the speed of sound through about a hundred meters of flame-heated tubing. The tubes are narrow to increase exposure to hot tube surfaces, but these surfaces invariably get covered in coke, which limits the heat transfer so severely that after weeks to months of operation, the plant must shut down for days of de-coking. A laser-based steam cracker could dispense with the narrow tubes, the coking shutdowns, and the powerful pumps—all because the laser transfers heat directly to the bulk fluid, with power densities orders of magnitude higher than those achievable in a traditional furnace.
 
At present, the economics of laser-based cracking look tricky given that electricity is an expensive form of heat. But the laser system might be a preferred solution in a greener future, or in a market willing to pay a premium for greener plastics.
 
Microwave sources could also be considered in a similar vein to lasers. Megawatt-scale magnetrons are expected to be 80% efficient and available <$1/W. These sources could volumetrically heat polar molecules, and may resist scattering from, e.g., nanoscale solid catalysts. 

‍

‍
References

[1]       A. H. Zewail, “Laser selective chemistry—is it possible?,” Physics Today, vol. 33, no. 11, pp. 27–33, Nov. 1980, doi: 10.1063/1.2913821.
[2]       A. Fridman, Plasma Chemistry. 2008.
[3]       G. L. Hill and T. G. Winter, “Effect of Temperature on the Rotational and Vibrational Relaxation Times of Some Hydrocarbons,” The Journal of Chemical Physics, vol. 49, no. 1, pp. 440–444, Jul. 1968, doi: 10.1063/1.1669842.
[4]       T. Ren, C. Wu, Y. Yu, T. Dai, F. Chen, and Q. Pan, “Development Progress of 3–5 μm Mid-Infrared Lasers: OPO, Solid-State and Fiber Laser,” Applied Sciences, vol. 11, no. 23, p. 11451, Dec. 2021, doi: 10.3390/app112311451.
[5]       M. C. Lin and M. H. Back, “THE THERMAL DECOMPOSITION OF ETHANE: PART I. INITIATION AND TERMINATION STEPS,” Can. J. Chem., vol. 44, no. 4, pp. 505–514, Feb. 1966, doi: 10.1139/v66-068.
[6]       Laidler, K. J., Chemical Kinetics, 3rd ed. Pearson, 1987.
[7]       Laidler, K. J., “Kinetics and mechanisms of the thermal decomposition of ethane - I. The uninhibited reaction,” Proc. R. Soc. Lond. A, vol. 260, no. 1300, pp. 91–102, Feb. 1961, doi: 10.1098/rspa.1961.0015.
[8]       M. C. Lin and M. H. Back, “THE THERMAL DECOMPOSITION OF ETHANE: PART III. SECONDARY REACTIONS,” Can. J. Chem., vol. 44, no. 20, pp. 2369–2380, Oct. 1966, doi: 10.1139/v66-358.
[9]       P. B. R. Nisbet-Jones et al., “Is the destruction or removal of atmospheric methane a worthwhile option?,” Phil. Trans. R. Soc. A., vol. 380, no. 2215, p. 20210108, Jan. 2022, doi: 10.1098/rsta.2021.0108.
[10]     A. W. Jasper, R. Sivaramakrishnan, and S. J. Klippenstein, “Nonthermal rate constants for CH4* + X → CH 3 + HX, X = H, O, OH, and O 2,” J. Chem. Phys., vol. 150, no. 11, p. 114112, Mar. 2019, doi: 10.1063/1.5090394.
[11]     S. N. Yurchenko, J. Tennyson, J. Bailey, M. D. J. Hollis, and G. Tinetti, “Spectrum of hot methane in astronomical objects using a comprehensive computed line list,” Proc. Natl. Acad. Sci. U.S.A., vol. 111, no. 26, pp. 9379–9383, Jul. 2014, doi: 10.1073/pnas.1324219111.